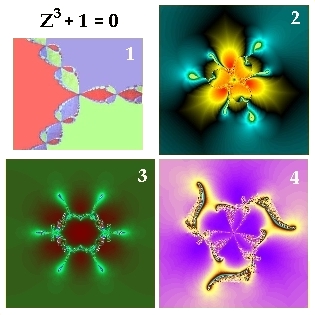
Wann treten Fraktale in der mathematischen
Rekursion (Rückkopplung) auf ?

Kompensation für Zyklus und Rhythmus

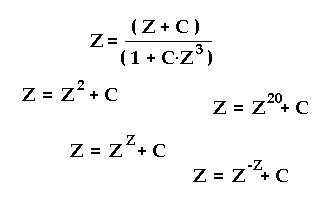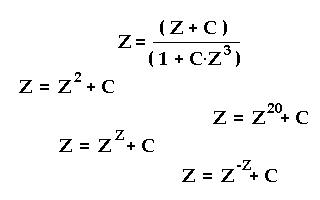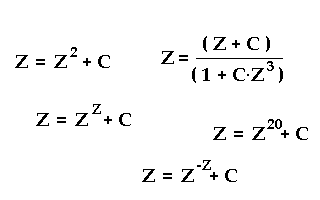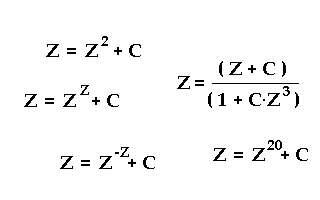
Ob es überhaupt ein Muster mit scharfen Grenzen gibt, hängt vom Aufbau der iterativen Funktion ab.

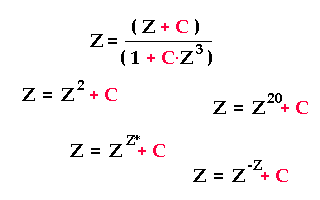
Mindestens eine Subtraktion muss in der Funktion vorhanden sein, um durch Kompensation von Teilgrößen in wiederkehrende Zyklen zu gelangen. Man beachte, dass Z und C genauso oft negative Komponenten haben können wie positive. Und wenn Z kleiner als Eins ist, verhält sich Z^2 wie sonst ein 1/(Z^2).

Dort, wo keine Kompensation stattfinden kann, bleiben die typischen selbstähnlichen fraktalen Muster aus.

Um einen Bezug zur Realität zu finden, sollte man mit realen Rückkopplungen vergleichen. Die Addition der festen Größe C in jeder Rechnungsschleife kann auch als fester Emmissions- oder Absorptionsbetrag pro Zeiteinheit aufgefasst werden.
Immer, wenn der addierte Betrag genau passt, um in einer der Rückkopplungen einen früheren Wert exakt wieder zu erreichen, erscheint zyklisches Verhalten im betrachteten Bildpunkt. Trifft ähnliches Verhalten auch auf Nachbarpunkte zu, entstehen Linien oder Flächen gleicher Farbe, die dem gleichen Rhythmus folgen.

Auf Rückkopplungsschaltungen in der Elektrotechnik übertragen, müssen gewisse parallel angeordnete und in Reihe angeordnete Bauelemente zusammenwirken (Invertierungen und Additionen), um einen interessanten Attraktor zu erzeugen. Biosysteme und ihre organischen Strukturen, wie etwa Muskeln, Gefäße und Nerven, sind immer gleichzeitig parallel und in Reihe angeordnet.

Rhythmisches Verhalten ist eine Grundlage von Leben, auch Rhythmen, die uns chaotisch erscheinen, und die erst später oder nie in die Ordnung finden.

Dünne Linien sind schmale Zahlenfenster, wie im Frequenzraum die Linien für Absorption oder Emission. Oft schachteln sie sich ineinander, wie einzelne Spektrallinien, die immer feiner aufspalten...

Vielfalt durch Disharmonie mit System

In dem eben gesehenen Fraktal wurde für die dritte Wurzel aus Eins das Newtonverfahren, ein optimales numerisches Lösungsverfahren, benutzt, aber stark verändert. Es wurden absichtlich Fehler eingebaut.

Die Harmonie wurde gestört, der optimale Lösungsvorgang unterlag Beschränkungen, ihm fehlten Freiheitsgrade der Bewegung.

Der schnellste Weg zum Ziel wurde gestört, immer wieder verhindert, bis sich andere Lösungen ergaben, neue Lösungen, die nicht mehr drei große Einzugsbereiche haben, die bis nach Unendlich reichen, sondern viele kleine, in der Nähe von Null bis 5.

weiter

Übersicht